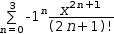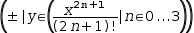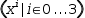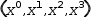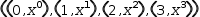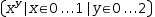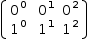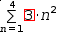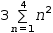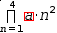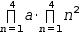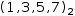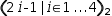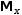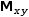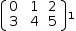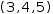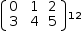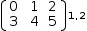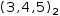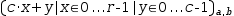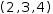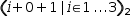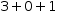6.3 Generators

Generators summarize two kinds of expressions: series and collections. A generator can be expanded into the expression it summarizes using Distribute . Individual elements of a collection generator can be extracted using indexing. Collection generators can serve as an indexable source in place of their expansion. For the syntax of generators, see §2.8.3.

6.3.1 Distribute

The result of expanding a series generator using Distribute is an expression consisting of operands joined by binary operators. The expansion of a collection generator is a set, a tuple or a matrix. A generator can only be expanded in this way if the limits are manifest expressions. Such generators are said to be iterable.

For example, the first few terms of Taylor's series for sin are given by 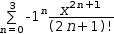∑0, 3, -1^n⋅(x^(2⋅n+1)÷(2⋅n+1) !)ⅆn. After symbolic Distribute and algebraic Simplify , the expression becomes x÷1 !-x^3÷3 !+x^5÷5 !-x^7÷7 !.

Alternating series are also created by using ± as the operator in a generalized series. The Taylor's series shown above can be generated by 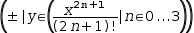(±|y∈(x^(2⋅n+1)÷(2⋅n+1) !|n∈0, 3)).

The result of expanding an iterable tuple generator is a tuple. The expansion of 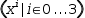(x^i|i∈0, 3) is 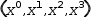(x^0, x^1, x^2, x^3). The generator body can itself contain a tuple or any other kind of expression. The expansion of ((i, x^i)|i∈0, 3) is 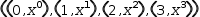((0, x^0), (1, x^1), (2, x^2), (3, x^3)).

A matrix generator expands into a matrix. 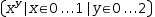[x^y|x∈0, 1|y∈0, 2] expands to 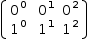[(0^0, 0^1, 0^2), (1^0, 1^1, 1^2)].

6.3.2 Manipulate

Simple series generators can be manipulated by left and right moves. For example, 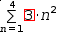∑1, 4, .{3}⋅n^2ⅆn and ← produce 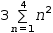3⋅∑1, 4, n^2ⅆn. 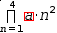∏1, 4, .{a}⋅n^2ⅆn and ← produce 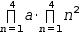(∏1, 4, aⅆn)⋅∏1, 4, n^2ⅆn.

6.3.3 Collections and Indexing

Indexing takes the form expression [ index ] and displays as expressionʈ[index]. The index can be a comma-separated list of expressions.

Ordered collections, along with their generators and iterators, are called indexable collections. Sets, and hence set generators, are not indexable collections because sets are not ordered. Scalars are not indexable because they are not collections. Thus only tuples and matrices are indexable collections. The general rule is that an indexed expression can be simplified if the expression is an indexable iterable collection and the index evaluates to a real constant, .

For example, the tuple and index expression 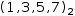(1, 3, 5, 7)[2] simplifies to 5. The same tuple can be generated and indexed by 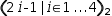(2⋅i-1|i∈1, 4)[2]. An intermediate result can be displayed by selecting just the generator .{(2⋅i-1|i∈1, 4)}[2] and expanding it.

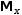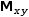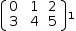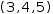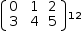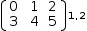A similar example illustrates indexing for matrices. Note here the distinction between Mɱ[x], Mɱ[x, y] and Mɱ[x][y]. The latter form provides a way to simplify just the first dimension of a matrix, yielding an indexed array generator as a result. [(0, 1, 2), (3, 4, 5)][1] is (3, 4, 5). With a double index, [(0, 1, 2), (3, 4, 5)][1][2] is 5, as is [(0, 1, 2), (3, 4, 5)][1, 2] but .{[(0, 1, 2), (3, 4, 5)][1]}[2] is 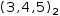(3, 4, 5)[2].

The preceding examples uses numeric values and simplification to show the operation of indexing. The dimensions and indexes of matrices can also be represented by unbound variables. However, only Evaluate can be used to bind variables to other expressions on the display. In the presence of a=1, b=2, r=2 and c=3, The expression 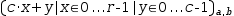[c⋅x+y|x∈0, r-1|y∈0, c-1][a, b] evaluates to 5

6.3.4 Generators and Indexing

Like other constructs in Myron, indexing is dynamically applied. An expression like aɱ[1, 2, 3] cannot be evaluated until a is given a value either through substitution or binding. Because a is not known, the number of indexes cannot be known in advance. If the indexed expression is composed of many indexable items, the expression is reduced by applying indexes one at a time until either the result is a scalar or no indexes remain.

To illustrate, consider a matrix of tuples.

Applied to this matrix, the index [0,1,2] (or [0][1][2]) produces value 4. The first two indexes select the element in the 0^th row and 1^st column to produce the tuple 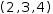(2, 3, 4). This tuple, indexed by 2, produces the value 4.

A more interesting example occurs when the same matrix is produced by indexing a generator.

The indexes have been separated so the effect of incremental simplification can be seen. Applied to the entire expression, the result is the same as if the index was [0,1,2]. But with the incremental indexes, simplifying the generator and the first index produces a tuple generator nested with a tuple generator: ((i+0+c|i∈1, 3)|c∈0, 2)[1][2]. Simplifying the expression and the first index again produces another tuple generator 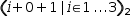(i+0+1|i∈1, 3)[2]. Final simplification produces 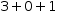3+0+1.